Chapitre 16 L’équilibre chimique

• Expliquer la notion d’équilibre chimique et comment elle est liée aux vitesses de réaction.
• Écrire l’expression de la constante d’équilibre associée à une équation chimique.
• Prédire le sens d’une réaction à partir de la constante d’équilibre et des concentrations des réactifs et produits.
• Calculer les concentrations d’équilibre à partir de la constante d’équilibre et de concentrations.
• Utiliser le principe de Le Châtelier pour prévoir l’évolution d’un système chimique à l’équilibre.

Dans le cas d’une réaction irréversible, les réactifs sont consommés et les produits sont produits. C’est ce que nous avons appelé la réaction directe. Dans le cas d’une réaction réversible, les produits peuvent également être consommés pour produire des réactifs. C’est ce que nous avons appelé la réaction indirecte. Un équilibre chimique est un état de la réaction dans lequel les réactions directe et indirecte se produisent à la même vitesse et où les concentrations des réactifs et des produits ne varient pas avec le temps.

Équilibre chimique
Un équilibre chimique est un état dans lequel la vitesse de la réaction directe est égale à celle de la réaction indirecte.

Considérons par exemple la décomposition du tétroxyde de diazote (N₂O₄) en dioxyde d’azote (NO₂). Ce processus, comme beaucoup de réactions chimiques, est réversible :

\[ N_2O_4\ {}_{(g)} \leftrightharpoons 2\ NO_2\ {}_{(g)} \]

N₂O₄ est un gaz incolore, alors que NO₂ est un gaz de couleur brun orangé.

Pour étudier cet équilibre, nous allons considérer la cinétique de la réaction. Les réactions directe et indirecte s’effectuent en une seule étape, nous pouvons donc écrire les lois de vitesse de chaque réaction :

\[ \begin{split} v_{directe} = k_{directe} \cdot |N_2O_4| \end{split} \qquad \text{ et } \qquad \begin{split} v_{indirecte} = k_{indirecte} \cdot |NO_2|^2 \end{split} \]

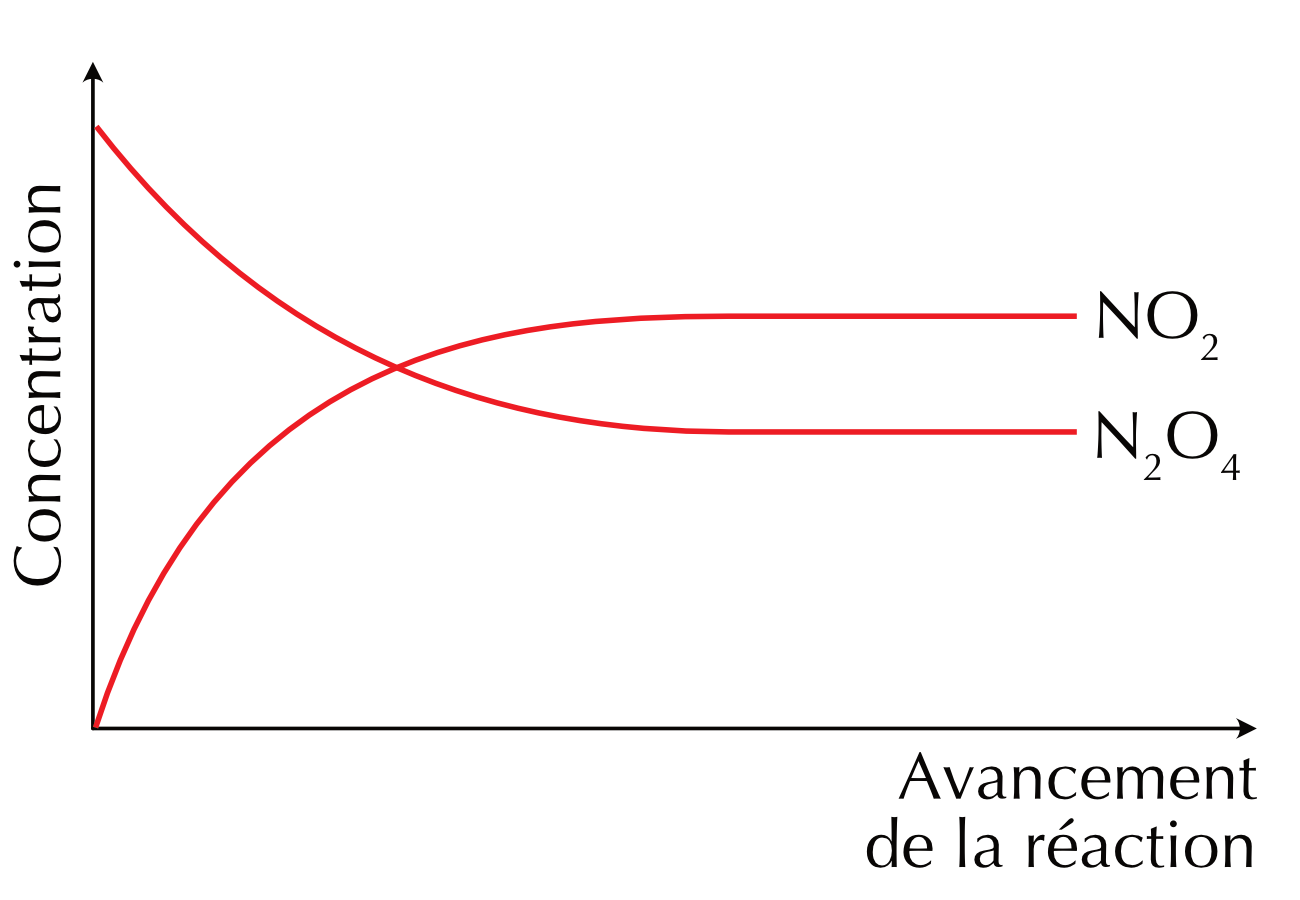
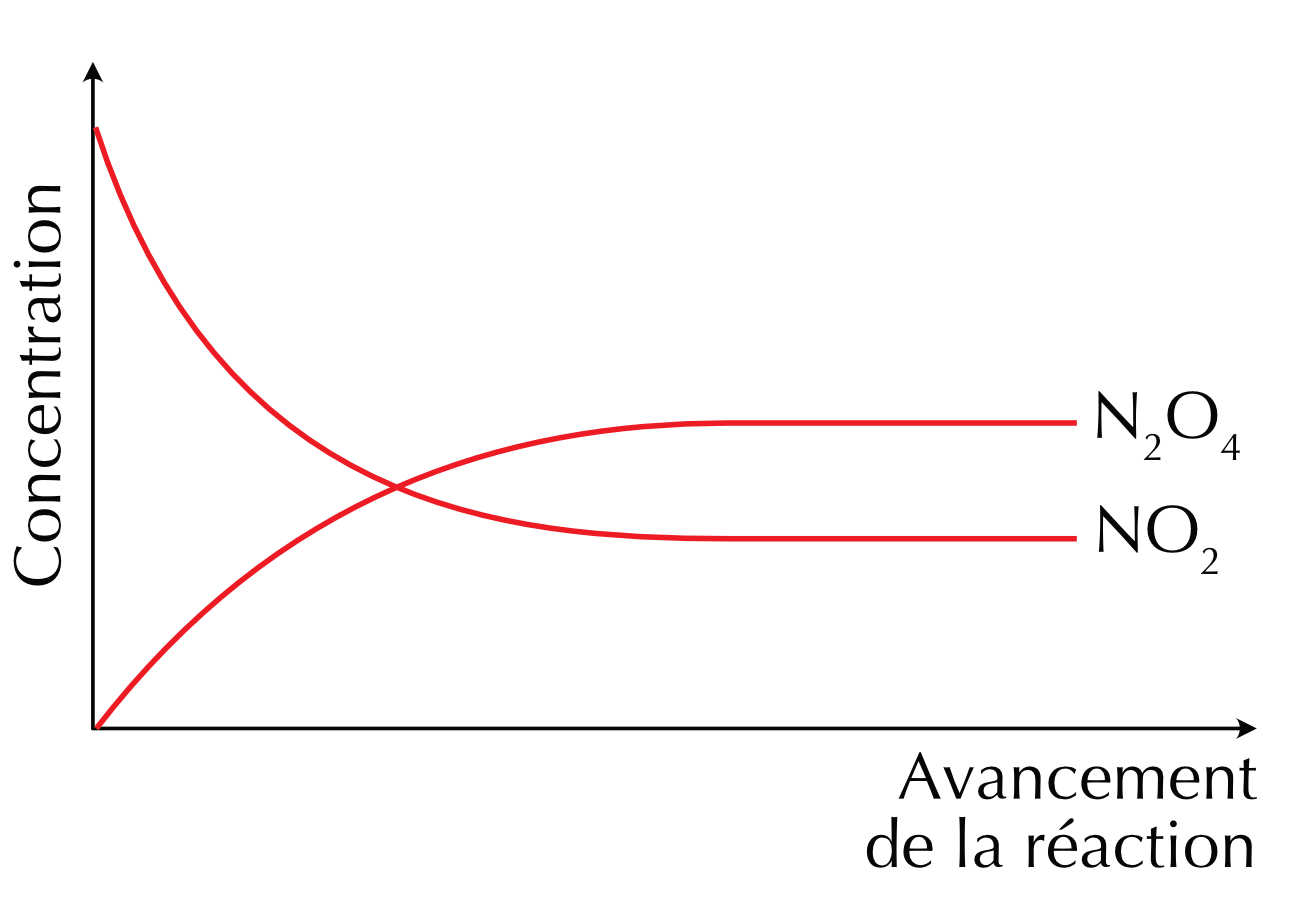
Figure 16.1: Profiles de la concentration en fonction du temps de la réaction directe et indirecte

Le terme équilibre est généralement employé pour décrire un état sans changement. Ce type d’équilibre est un état d’équilibre statique puisqu’il caractérise l’état d’un système immobile. Cependant, un système à l’équilibre n’est pas toujours sans changement, comme, justement, un équilibre chimique.

À l’échelle macroscopique, on ne voit pas de changement alors qu’à l’échelle sub-microscopique les réactions directes et indirectes continuent d’avoir lieu. Les vitesses directe et indirecte sont non-nulles et égales.

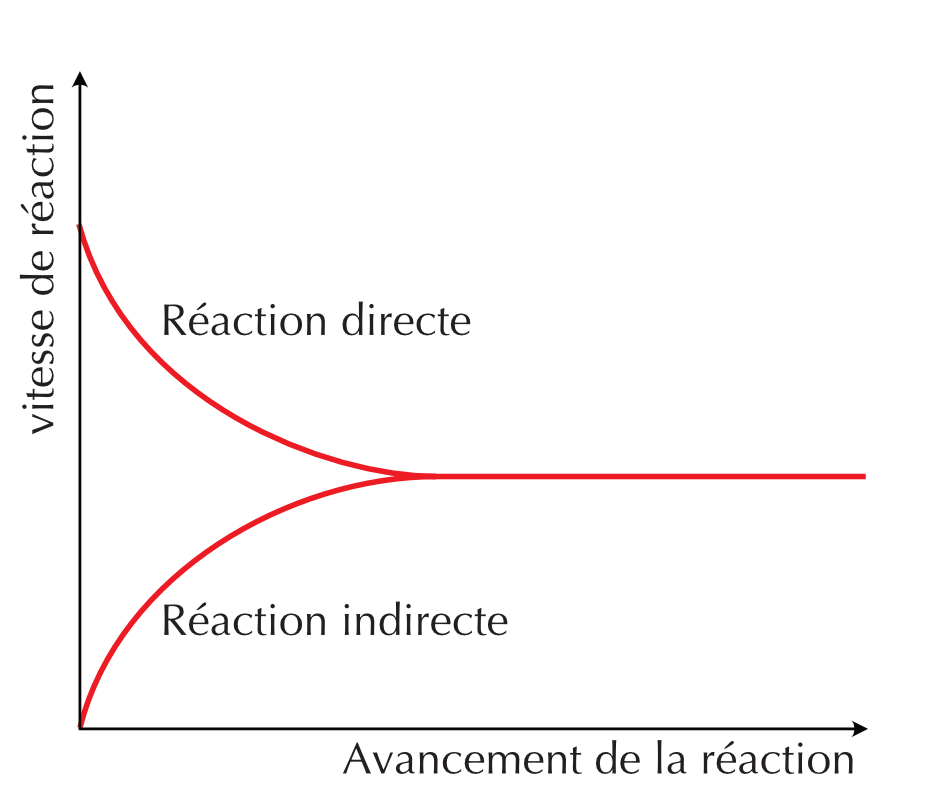
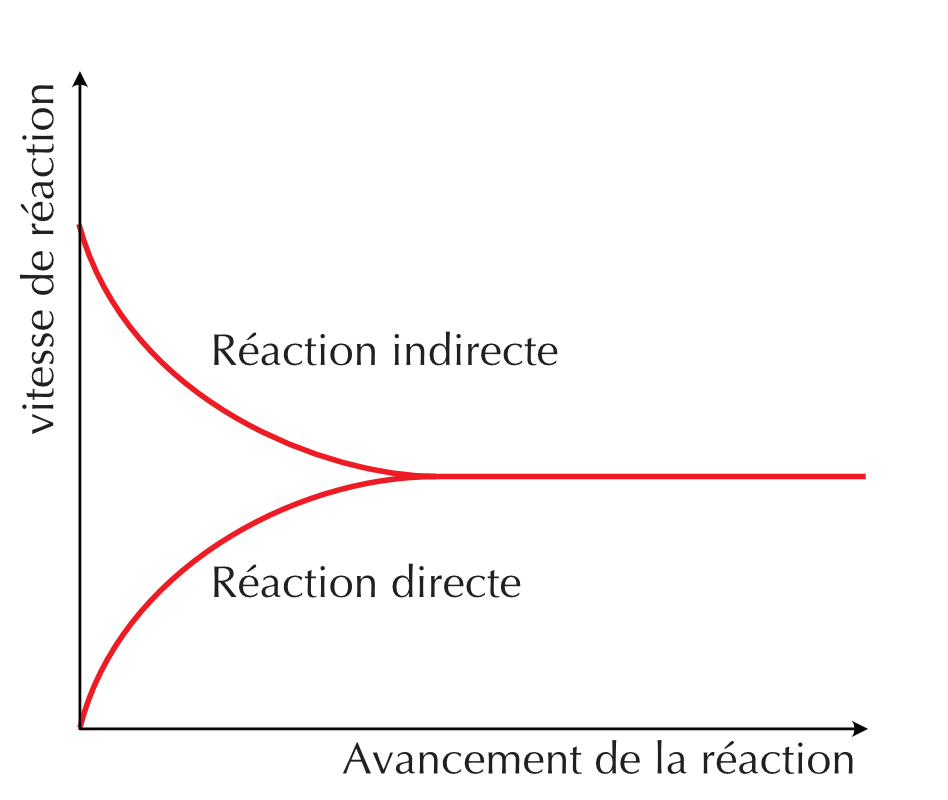
Figure 16.2: Profiles de la vitesse de réaction en fonction du temps de la réaction directe et indirecte

Un état d’équilibre chimique est appelé état d’équilibre dynamique car, bien que les concentrations de réactifs et de produits ne varient pas avec le temps, les réactions directe et indirecte continuent de se produire.

16.1 Le quotient de réaction

Au milieu du XIX^e siècle, Cato Guldberg et Peter Waage ont étudié les équilibres chimiques d’une grande variété de réactions. Ils ont observé qu’à température constante, dans un mélange à l’équilibre de réactifs et de produits, quelles que soient les concentrations initiales, le quotient de réaction a une valeur constante.

Le quotient de réaction (Q_r) est une grandeur qui permet de caractériser un système chimique. Il est défini comme le quotient du produit des concentrations des produits et du produit des concentrations des réactifs, chaque concentration étant portée à une puissance égale au coefficient stœchiométrique correspondant de l’équation chimique équilibrée. Cette grandeur nous donne une information sur les quantités relatives de produits et de réactifs lors d’une réaction à un instant t.

Considérons un système chimique à l’équilibre, dont les espèces sont toutes dissoutes dans l’eau et dont l’équation de la réaction est la suivante :

\[ a\ A_{(aq)} + b\ B_{(aq)} \leftrightharpoons c\ C_{(aq)} + d\ D_{(aq)} \]

Par définition, le quotient de réaction de cette transformation s’écrit :

\[ Q_{r}(t) = \frac{|C|_{(t)}^{c} \cdot |D|_{(t)}^{d}}{|A|_{(t)}^{a} \cdot |B|_{(t)}^{b}} \]

Les concentrations des espèces dissoutes sont exprimées en mole par litre (mol/l).

16.2 La constante d’équilibre

À l’équilibre, les concentrations des réactifs et des produits ne varient plus ce qui implique que le quotient de réaction ne varie plus, lui non plus. Il devient constant. On appellera la valeur de Q_r à l’équilibre, constante d’équilibre (K_c).

\[ Q_{r}(eq) = K_{c} = \frac{|C|_{(eq)}^{c} \cdot |D|_{(eq)}^{d}}{|A|_{(eq)}^{a} \cdot |B|_{(eq)}^{b}} \]

• Comme le quotient de réaction, la constante d’équilibre n’a pas de dimension et s’exprime sans unité.
• Une constante d’équilibre élevée (K_c > 10³) indique que les produits sont favorisés à l’équilibre.
• Une constante d’équilibre faible (K_c < 10^-3) indique que les réactifs sont favorisés à l’équilibre.
• K_c ne dépend que de la température.

La valeur de K_c peut donc être calculée lorsque l’on a mesuré les concentrations des réactifs et produits à l’équilibre pour une température donnée. Pour simplifier l’écriture, à l’équilibre, on pourra écrire :

\[ K_{c} = \frac{|C|^{c} \cdot |D|^{d}}{|A|^{a} \cdot |B|^{b}} \]

16.2.1 Équilibre homogène et hétérogène

Lorsque toutes les substances participant à la réaction sont dans la même phase, on parlera d’équilibre homogène et lorsque toutes les substances participant à la réaction sont dans des phases différentes, on parlera d’équilibre hétérogène.

Lors du calcul des constantes d’équilibre, les solides et les liquides purs ne sont pas pris en compte car leur concentration ne change pas au cours de la réaction.

16.2.2 Constantes d’équilibre et phase gazeuse

Nous avons exprimé jusqu’à présent les constantes d’équilibre en utilisant la concentration. Cependant, pour les réactions en phase gazeuse, nous pouvons exprimer les constantes d’équilibre en utilisant les pressions partielles des gaz impliqués.

La loi des pressions partielles exprime que la pression d’un gaz est directement proportionnelle à sa concentration (pour un volume et une température constants). Dans un mélange de gaz, la pression partielle d’un gaz composant le mélange est la pression avec laquelle il contribue à la pression totale.

Supposons la réaction en phase gazeuse générique équilibrée ci-dessous :

\[ a\ A_{(g)} + b\ B_{(g)} \leftrightharpoons c\ C_{(g)} + d\ D_{(g)} \]

Si nous connaissons les pressions partielles de chaque composant à l’équilibre, alors l’expression de la constante d’équilibre pour cette réaction peut-être expimée par la relation suivante :

\[ K_{p} = \frac{P_C^{c} \cdot P_D^{d}}{P_A^{a} \cdot P_B^{b}} \]

avec :

• P_A : pression partielle du gaz A dans le système.
• P_B : pression partielle du gaz B dans le système.
• …

Ecrivez l’expression de la constante d’équilibre pour les réactions suivantes. Dans chaque cas, indiquez si la réaction est homogène ou hétérogène.

1. \(3\ NO\ _{(g)} \leftrightharpoons N_2O\ _{(g)} + NO_2\ _{(g)}\)
2. \(CH_4\ _{(g)} + 2\ H_2S\ _{(g)} \leftrightharpoons CS_2\ _{(g)} + 4\ H_2\ _{(g)}\)
3. \(HF\ _{(aq)} \leftrightharpoons H^+\ _{(aq)} + F^-\ _{(aq)}\)
4. \(2\ NaHCO_3\ _{(s)} \leftrightharpoons Na_2CO_3\ _{(s)} + CO_2\ _{(g)} + H_2O\ _{(g)}\)
5. \(H_2O\ _{(l)} \leftrightharpoons H^+\ _{(aq)} + OH^-\ _{(aq)}\)
6. \(2\ Ag\ _{(s)} + Zn^{2+}\ _{(aq)} \leftrightharpoons 2\ Ag^+\ _{(aq)} + Zn\ _{(s)}\)

1. \[ K_{c} = \frac{|N_2O| \cdot |NO_2|}{|NO|^{3}} \qquad \text{(homogène)} \]
2. \[ K_{c} = \frac{|CS_2| \cdot |H_2|^{4}}{|CH_4| \cdot |H_2S|^{2}} \qquad \text{(homogène)} \]
3. \[ K_{c} = \frac{|H^+| \cdot |F^-|}{|HF|} \qquad \text{(homogène)} \]
4. \[ K_{c} = |CO_2| \cdot |H_2O| = P_{CO_2} \cdot P_{H_2O} \qquad \text{(homogène)} \]
5. \[ K_{c} = |H^+| \cdot |OH^-| \qquad \text{(hétérogène)} \]
6. \[ K_{c} = \frac{|Ag^+|^{2}}{|Zn^{2+}|} \qquad \text{(hétérogène)} \]

16.3 Équilibres chimiques et stœchiométrie

En cherchant à mesurer la constante d’équilibre de la décomposition de l’iodure d’hydrogène, on remplit un ballon sous vide de 2 [l] avec 0.2 [mol] de \(HI\) gazeux et on laisse la réaction se dérouler à 453°C.

\[ 2\ HI\ _{(g)} \leftrightharpoons H_2\ _{(g)} + I_2\ _{(g)} \]

À l’équilibre, on mesure une concentration en iodure d’hydrogène, \(|HI|_{eq}\) = 0.078 [M].

On commence par calculer la concentration initiale en iodure d’hydrogène, \(|HI|_{0}\).

\[ |HI|_0 = \frac{0.2\ [mol]}{2\ [l]} = 0.1\ [M] \]

On peut ensuite établir un tableau des variations :

Concentrations [M]	\(2\ HI\ _{(g)}\)	\(\leftrightharpoons\)	\(H_2\ _{(g)}\)	\(I_2\ _{(g)}\)
initiale	0.1		0	0
variation	- 2x		+ x	+ x
équilibre	0.1 - 2x		x	x

On connaît la valeur de la concentration de \(HI\) à l’équilibre. On peut donc résoudre l’équation pour x :

\[ |HI|_{eq} = 0.1\ [M] - 2 \cdot x = 0.078\ [M] \quad \rightarrow \quad x = 0.011\ [M] \]

Par conséquent, les concentrations à l’équilibre sont :

\[ |H_2|_{eq} = |I_2|_{eq} = 0.011\ [M] \quad \text{et} \quad |HI|_{eq} = 0.078\ [M] \]

On peut donc calculer la valeur de la constante d’équilibre de la réaction à 453°C.

\[ K_{c} = \frac{|H_2|_{eq} \cdot |I_2|_{eq}}{|HI|_{eq}^2} = \frac{0.011 \cdot 0.011}{0.078^2} = 0.02\ [-]\ \text{à 453°C} \]

On étudie la réaction entre l’ammoniac et le dioxygène

\[ 4\ NH_3\ _{(g)} + 7\ O_2\ _{(g)} \leftrightharpoons 2\ N_2O_4\ _{(g)} + 6\ H_2O\ _{(g)} \]

On remplit un ballon avec 2.4 [M] de NH₃ et 2.4 [M] de O₂ à une température donnée. La réaction se déroule et à l’équilibre on mesure une concentration en N₂O₄ égale à 0.134 [M]. Calculer K_c.

\[ \begin{split} \text{Concentrations [M]} &\\ \text{initiale} &\\ \text{variation} &\\ \text{équilibre} & \end{split} \quad \begin{split} 4\ NH_3\ _{(g)} &\\ 2.4 &\\ -4\ x &\\ 2.4 - 4x & \end{split} \quad \begin{split} 7\ O_2\ _{(g)} &\\ 2.4 &\\ -7\ x &\\ 2.4 - 7x & \end{split} \quad \begin{split} \leftrightharpoons &\\ ~ &\\ ~ &\\ ~ & \end{split} \quad \begin{split} 2\ N_2O_4\ _{(g)}\\ 0 &\\ +2\ x &\\ 2x & \end{split} \quad \begin{split} 6\ H_2O\ _{(g)}\\ 0 &\\ +6\ x &\\ 6x & \end{split} \]

\[ \begin{split} |N_2O_4|_{eq} &= 2x = 0.134\ [M] \\ \Rightarrow x &= 0.067\ [M] \\ |NH_3|_{eq} &= 2.4 – 4x = 2.4 – 4 \cdot 0.067 = 2.13\ [M] \\ |O_2|_{eq} &= 2.4 – 7x = 2.4 – 7 \cdot 0.067 = 1.93\ [M] \\ |H_2O|_{eq} &= 6x = 6 \cdot 0.067 = 0.402\ [M] \end{split} \]

\[ K_{c} = \frac{|N_2O_4|^{2}_{eq} \cdot |H_2O|^{6}_{eq}}{|NH_3|^{4}_{eq} \cdot |O_2|^{7}_{eq}} = \frac{(0.134)^2 \cdot (0.402)^{6}}{(2.13)^{4} \cdot (1.93)^{7}} = 3.69 \cdot 10^{−8}\ [-] \]

16.4 Évolution spontanée et principe de Le Châtelier

Le principe de Le Châtelier permet de prédire le sens de la réaction qui sera favorisé lorsqu’on modifie les conditions d’un système à l’équilibre.

“Lorsque les modifications extérieures apportées à un système physico-chimique en équilibre provoquent une évolution vers un nouvel état d’équilibre, l’évolution s’oppose aux perturbations qui l’ont engendrée et en modère l’effet.”

— Henry Louis Le Châtelier

Dit autrement : si on modifie les conditions d’un système à l’équilibre, il réagit de façon à s’opposer aux changements qu’on lui impose jusqu’à l’établissement d’un nouvel état d’équilibre.

Pour modifier un équilibre, on peut agir sur différents facteurs :

• L’addition d’un réactif ou d’un produit.
• L’élimination d’un réactif ou d’un produit.
• Un changement de volume ou de pression du système
  (pour les systèmes contenant des réactifs et des produits gazeux).
• Un changement de température.

16.4.1 Ajout/élimination d’un réactif ou d’un produit

Prenons en exemple la réaction du diazote avec le dihydrogène gazeux pour former l’ammoniac gazeux.

\[ N_2\ _{(g)} + 3\ H_2\ _{(g)} \leftrightharpoons 2\ NH_3\ _{(g)} \]

Selon le principe de Le Châtelier :

• L’ajout d’un réactif ou l’élimination d’un produit entraîne un déplacement de l’équilibre vers la droite.
• L’ajout d’un produit ou l’élimination d’un réactif entraîne un déplacement de l’équilibre vers la gauche.

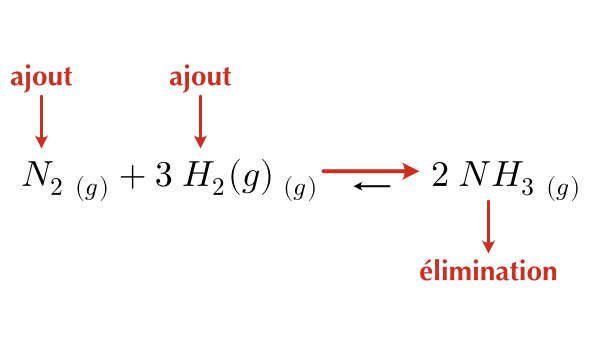
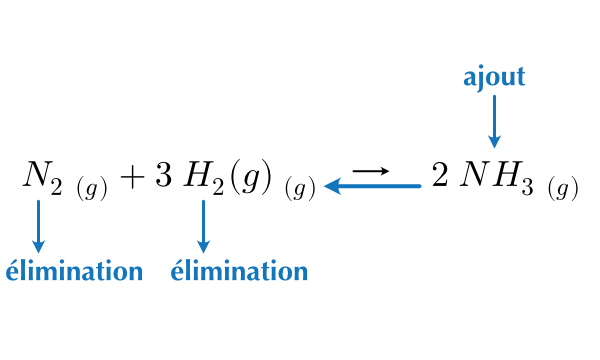
Figure 16.3: Effet de l’ajout/élimination de réactifs ou de produits sur le sens de la réaction

• Lorsqu’on ajoute une substance, la réaction déplace l’équilibre de manière à consommer une partie de cette substance.
• Lorsqu’on élimine une substance, la réaction déplace l’équilibre de manière à produire d’avantage de cette substance.

L’ajout ou le retrait d’une espèce d’une réaction à l’équilibre ne change pas la valeur de la constante d’équilibre K_c. Le rapport des concentrations rejoindra la même valeur qu’avant la modification.

16.4.2 Influence du volume et de la pression

Prenons en exemple la décomposition du tétroxyde de diazote (N₂O₄) en dioxyde d’azote (NO₂).

\[ N_2O_4\ {}_{(g)} \leftrightharpoons 2\ NO_2\ {}_{(g)} \]

Imaginons un cylindre fermé avec un piston mobile comme couvercle. L’équilibre ci-dessus se produit à l’intérieur du cylindre. En déplaçant le piston, on change le volume du système et on modifie les concentrations des réactifs et des produits. Si nous poussons sur le piston, l’équilibre sera perturbé et se déplacera dans la direction qui minimise l’effet de cette perturbation.

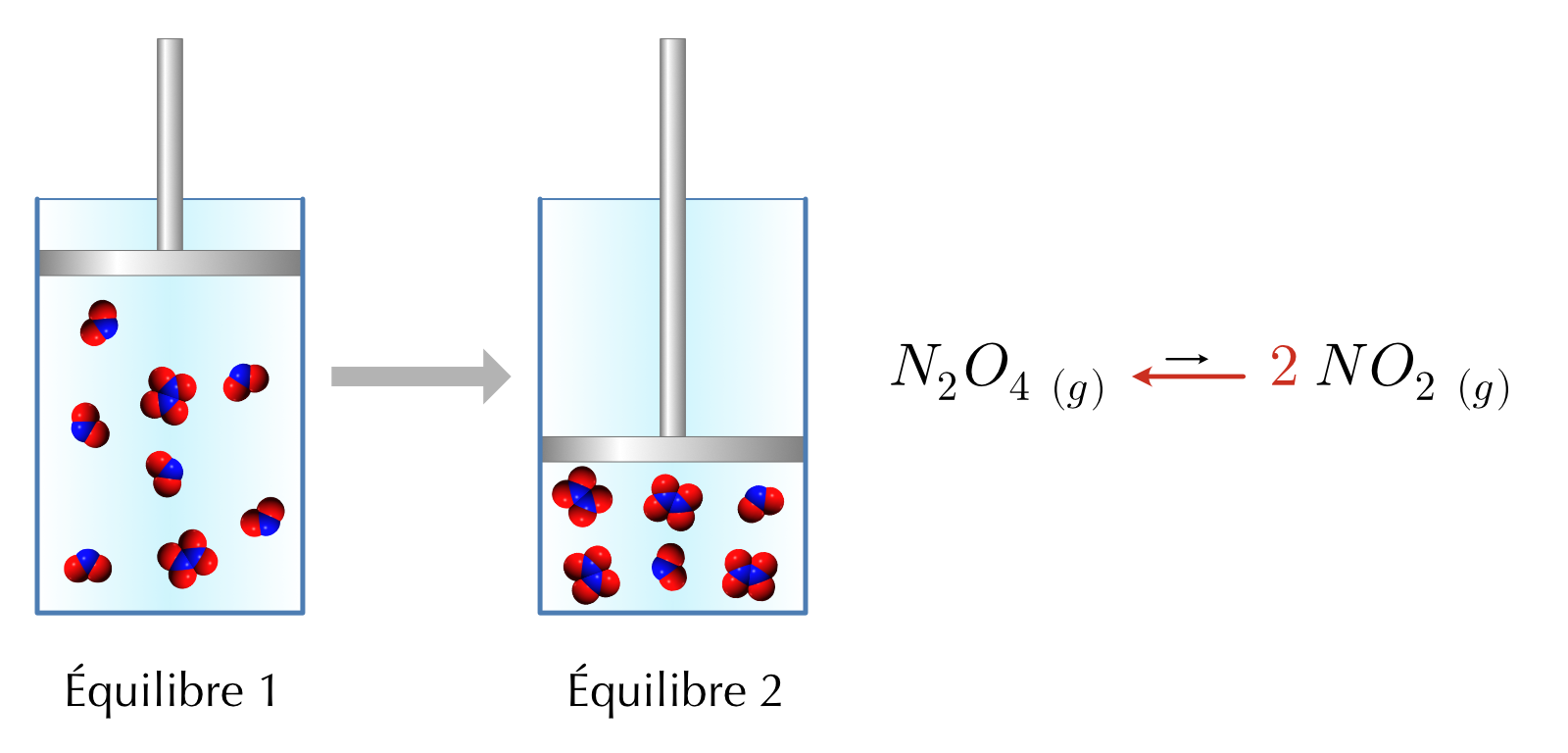
Figure 16.4: Effet de la diminution du volume (augmentation de la pression) sur l’équilibre

La réaction globale présente moins de moles de gaz du côté des produits. L’équilibre sera donc déplacé vers la gauche.

RAPPEL :

• Une augmentation du volume diminue la pression (\(V \uparrow\) - \(P \downarrow\)).
• Une diminution du volume augmente la pression (\(V \downarrow\) - \(P \uparrow\)).

En résumé :

Une diminution du volume de la réaction favorise la réaction (directe ou indirecte) qui diminue le nombre total de moles de gaz.

Une augmentation du volume de la réaction favorise la réaction (directe ou indirecte) qui augmente le nombre total de moles de gaz.

Si le même nombre de moles de gaz sont de chaque côté de l’équation chimique, une variation de volume (ou de pression) n’aura pas d’influence sur l’équilibre chimique.

16.4.3 Influence de la température

Un changement de concentration ou de volume peut déplacer un équilibre chimique mais il ne change pas la valeur de la constante d’équilibre. La température, par contre, influence un état d’équilibre chimique car elle modifie la valeur de la constante d’équilibre.

Dans la réaction suivante, le sens direct est endothermique (la réaction absorbe de la chaleur).

\[ \text{chaleur} + N_2O_4\ {}_{(g)} \leftrightharpoons 2\ NO_2\ {}_{(g)} \]

Si nous considérons la chaleur comme un réactif, nous pouvons appliquer le principe de Le Châtelier pour prédire dans quel sens sera déplacé l’équilibre si nous ajoutons ou retirons de la chaleur.

L’augmentation de la température (apport de chaleur) déplacera la réaction dans le sens direct, car la chaleur apparaît du côté du réactif. La diminution de la température (retrait de chaleur) déplacera la réaction dans le sens indirect.

En résumé :

Une augmentation de la température favorise le sens endothermique (direct ou indirect) d’un équilibre chimique.

Une diminution de la température favorise le sens exothermique (direct ou indirect) d’un équilibre chimique.

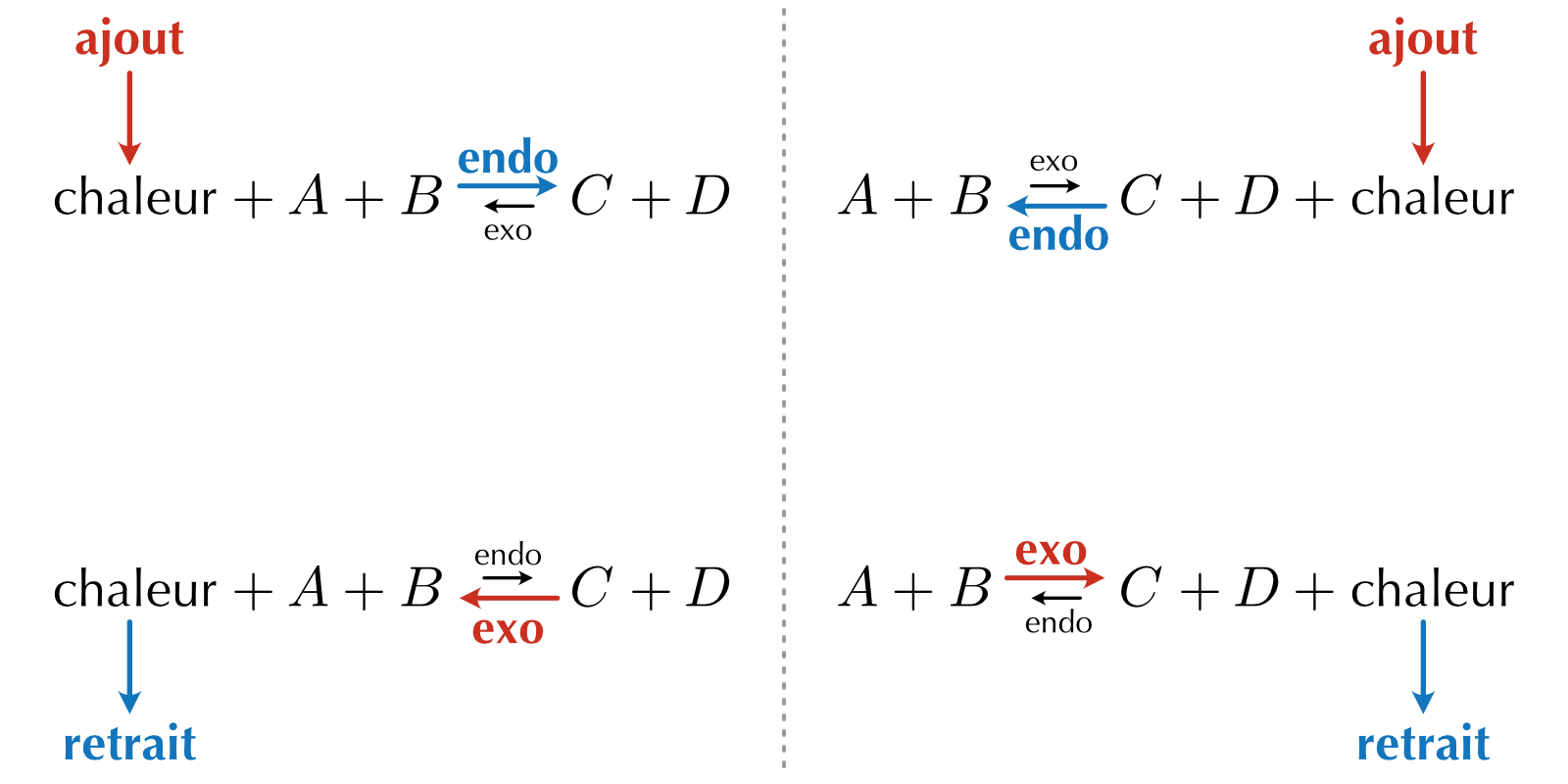
Figure 16.5: Effet de l’ajout ou le retrait de chaleur sur l’équilibre

16.4.4 Effet d’un catalyseur sur un équilibre chimique

Un catalyseur accélère une réaction en abaissant l’énergie d’activation de la réaction. Cependant il abaisse l’énergie d’activation de la réaction directe ainsi que de la réaction indirecte, et ceci dans la même mesure. La présence d’un catalyseur ne modifie donc pas la constante d’équilibre, ni ne modifie les quantités de matières de réactifs et de produits.

L’ajout d’un catalyseur à une réaction ne modifie pas un équilibre chimique.

Si un catalyseur est ajouté à un mélange réactionnel qui n’est pas à l’équilibre le mélange atteindra l’équilibre plus rapidement.

\[ 2\ SO_2\ _{(g)} + O_2\ _{(g)} \leftrightharpoons 2\ SO_3\ _{(g)} + \text{chaleur} \]

Dans la réaction ci-dessus, on favorise le rendement en SO₃ :

1. lorsque l’on augmente ou abaisse la pression ? (justifiez)
2. lorsque l’on augmente ou abaisse la température ? (justifiez)

1. L’équilibre est favorisé à droite en augmentant la pression pour réduire le nombre total de moles de gaz.
2. L’équilibre est favorisé à droite en abaissant la température pour favoriser le sens exothermique.

\[ C\ _{(s)} + 2\ H_2\ _{(g)} \leftrightharpoons CH_4\ _{(g)} + \text{chaleur} \]

Quels sont les effets des changements énoncés ci-dessous sur cet équilibre chimique ?

1. Une augmentation de température. (justifiez)
2. Une augmentation de la pression en diminuant le volume. (justifiez)
3. Permettre au CH₄ de s’échapper en continu du réacteur abritant la réaction. (justifiez)

1. L’équilibre favorise la production de réactifs en favorisant le sens exothermique de la réaction.
2. L’équilibre favorise la production de produits pour diminuer le nombre totale de moles de gaz.
3. L’équilibre favorise la production de produits de manière à produire plus de CH₄.

16.5 Exercices supplémentaires

De l’oxychlorure d’azote pur (\(\ce{NOCl}\)) gazeux est chauffé à 240°C dans un récipient de 1 L et donne lieu à l’équilibre chimique suivant :

\[ \ce{2 NOCl_{(g)} <=> 2 NO_{(g)} + Cl_{2(g)}} \]

À l’équilibre, la pression totale est de 1 atm et la pression du \(\ce{NOCl}\) est de 0.64 atm.

1. Calculer les pressions partielles de et de dans le système.
2. Calculer la constante d’équilibre K_p.

1. \[ \begin{split} P_{Tot} &= P_{\ce{NOCl}} + P_{\ce{NO}} + P_{\ce{Cl2}} \\ P_{\ce{NO}} + P_{\ce{Cl2}} &= P_{Tot} - P_{\ce{NOCl}} \\ &= 1\ [atm] - 0.64\ [atm] = 0.36\ [atm] \end{split} \qquad \begin{split} \frac{n_{\ce{NO}}}{n_{\ce{Cl2}}} &= \frac{2}{1} \\ P_{\ce{NO}} &= 2 \cdot P_{\ce{Cl2}} \end{split} \]

\[ \begin{split} P_{\ce{NO}} &= \frac{2}{3} \cdot 0.36\ [atm] = 0.24\ [atm] \\ P_{\ce{Cl2}} &= \frac{1}{3} \cdot 0.36\ [atm] = 0.12\ [atm] \end{split} \]

2. \[ \begin{split} K_{p} = \frac{P_{\ce{NO}}^2 \cdot P_{\ce{Cl2}} }{P_{\ce{NOCl}}^2} = \frac{(0.24)^2\ [atm] \cdot 0.12\ [atm]}{(0.64)^2\ [atm]} = 0.017\ [-] \end{split} \]